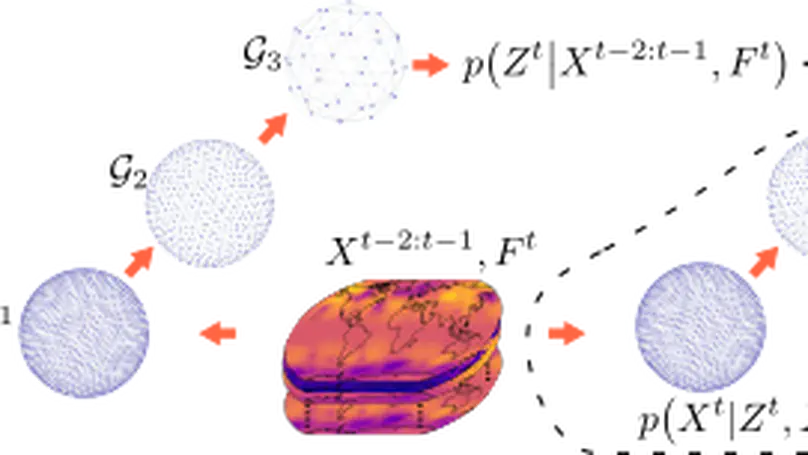
In recent years, machine learning has established itself as a powerful tool for high-resolution weather forecasting. While most current machine learning models focus on deterministic forecasts, accurately capturing the uncertainty in the chaotic weather system calls for probabilistic modeling. We propose a probabilistic weather forecasting model called Graph-EFM, combining a flexible latent-variable formulation with the successful graph-based forecasting framework. The use of a hierarchical graph construction allows for efficient sampling of spatially coherent forecasts. Requiring only a single forward pass per time step, Graph-EFM allows for fast generation of arbitrarily large ensembles. We experiment with the model on both global and limited area forecasting. Ensemble forecasts from Graph-EFM achieve equivalent or lower errors than comparable deterministic models, with the added benefit of accurately capturing forecast uncertainty.

Global convolutions have shown increasing promise as powerful general-purpose sequence models. However, training long convolutions is challenging, and kernel parameterizations must be able to learn long-range dependencies without overfitting. This work introduces reparameterized multi-resolution convolutions (MRConv), a novel approach to parameterizing global convolutional kernels for long-sequence modelling. By leveraging multi-resolution convolutions, incorporating structural reparameterization and introducing learnable kernel decay, MRConv learns expressive long-range kernels that perform well across various data modalities. Our experiments demonstrate state-of-the-art performance on the Long Range Arena, Sequential CIFAR, and Speech Commands tasks among convolution models and linear-time transformers. Moreover, we report improved performance on ImageNet classification by replacing 2D convolutions with 1D MRConv layers.

Unlike traditional rigid robots, soft robots offer more flexibility, compliance, and adaptability. They are also typically cheaper to manufacture and are lighter than their rigid counterparts. However, due to modeling difficulties, real-world applications for soft robots are still limited. This is especially true for applications that would require dynamic or fast motion. In addition, their operating principles and compliance make integrating effective proprioceptive sensors difficult. As such, state estimation and predictions of how the state evolves in time are challenging modeling tasks. Large-scale ($≈$ two meters in length), particularly fluid-driven, soft robots have greater modeling complexity due to increased inertia and related effects of gravity. Few approaches to soft robot control (learned or model-based) have enabled dynamic motion such as throwing or hammering since most methods require limiting assumptions about the kinematics, dynamics, or actuation models to make the control problem tractable or performant. To address this issue, we propose using Bayesian optimization to learn policies for dynamic tasks on a large-scale soft robot. This approach optimizes the task objective function directly from commanded pressures, without requiring approximate kinematics or dynamics as an intermediate step. We also present simulated and real-world experiments to illustrate the efficacy of the proposed approach.

In this work, we present a new open-source Python programming library for performing efficient interpolation of non-stationary satellite altimetry data, using scalable Gaussian Process (GP) techniques. We showcase the library, GPSat, by using data from the CryoSat-2, Sentinel-3A, and Sentinel-3B radar altimeters, to generate complete maps of daily 50 km$^2$-gridded Arctic sea ice radar freeboard. Relative to a previous GP interpolation scheme, we find that GPSat offers a 504$times$ computational speedup, with less than 4 mm difference on the derived freeboards, on average. We then demonstrate the scalability of GPSat through freeboard interpolation at 5 km$^2$ grid resolution, and Sea-Level Anomalies (SLA) at the resolution of the altimeter footprint. Validation of this novel high resolution radar freeboard product shows strong agreement with airborne data, with a linear correlation of 0.66. Footprint-level SLA interpolation also shows improvements in predictive skill over linear regression, which is a standard approach used in sea ice altimetry data processing. We suggest that GPSat could overcome the computational bottlenecks faced in many altimetry-based interpolation routines. This could in turn lead to improved observational estimates of ocean topography and sea ice thickness, and also further critical understanding of ocean and sea ice variability over short spatio-temporal scales.

In recent years, there has been considerable interest in developing machine learning models on graphs to account for topological inductive biases. In particular, recent attention has been given to Gaussian processes on such structures since they can additionally account for uncertainty. However, graphs are limited to modelling relations between two vertices. In this paper, we go beyond this dyadic setting and consider polyadic relations that include interactions between vertices, edges and one of their generalisations, known as cells. Specifically, we propose Gaussian processes on cellular complexes, a generalisation of graphs that captures interactions between these higher-order cells. One of our key contributions is the derivation of two novel kernels, one that generalises the graph Matérn kernel and one that additionally mixes information of different cell types.